Like BST Operations, commonly performed operations on AVL tree are-
- Search Operation
- Insertion Operation
- Deletion Operation
- Step 1 - Read the search element from the user.
- Step 2 - Compare the search element with the value of root node in the tree.
- Step 3 - If both are matched, then display "Given node is found!!!" and terminate the function
- Step 4 - If both are not matched, then check whether search element is smaller or larger than that node value.
- Step 5 - If search element is smaller, then continue the search process in left subtree.
- Step 6 - If search element is larger, then continue the search process in right subtree.
- Step 7 - Repeat the same until we find the exact element or until the search element is compared with the leaf node.
- Step 8 - If we reach to the node having the value equal to the search value, then display "Element is found" and terminate the function.
- Step 9 - If we reach to the leaf node and if it is also not matched with the search element, then display "Element is not found" and terminate the function.
- Step 1 - Insert the new element into the tree using Binary Search Tree insertion logic.
- Step 2 - After insertion, check the Balance Factor of every node.
- Step 3 - If the Balance Factor of every node is 0 or 1 or -1 then go for next operation.
- Step 4 - If the Balance Factor of any node is other than 0 or 1 or -1 then that tree is said to be imbalanced. In this case, perform suitable Rotation to make it balanced and go for next operation.
We perform rotation in AVL tree only in case if Balance Factor is other than -1, 0, and 1.
- L L rotation: Inserted node is in the left subtree of left subtree of A
- R R rotation : Inserted node is in the right subtree of right subtree of A
- L R rotation : Inserted node is in the right subtree of left subtree of A
- R L rotation : Inserted node is in the left subtree of right subtree of A
Where node A is the node whose balance Factor is other than -1, 0, 1.
The first two rotations LL and RR are single rotations and the next two rotations LR and RL are double rotations.
In above example, node C has balance factor 2 because a node A is inserted in the left subtree of C left subtree. We perform the LL rotation on the edge below A.
When BST becomes unbalanced, due to a node is inserted into the right subtree of the right subtree of A, then we perform RR rotation, RR rotation is an anticlockwise rotation, which is applied on the edge below a node having balance factor -2.
In above example, node A has balance factor -2 because a node C is inserted in the right subtree of A right subtree. We perform the RR rotation on the edge below A.
Double rotations are bit tougher than single rotation which has already explained above. LR rotation = RR rotation + LL rotation, i.e., first RR rotation is performed on subtree and then LL rotation is performed on full tree, by full tree we mean the first node from the path of inserted node whose balance factor is other than -1, 0, or 1.
Let us understand each and every step very clearly:
RL Rotation
As already discussed, that double rotations are bit tougher than single rotation which has already explained above. R L rotation = LL rotation + RR rotation, i.e., first LL rotation is performed on subtree and then RR rotation is performed on full tree, by full tree we mean the first node from the path of inserted node whose balance factor is other than -1, 0, or 1.
Example
Construct an AVL tree having the following elements
H, I, J, B, A, E, C, F, D, G, K, L
Solution
On inserting the above elements, especially in the case of H, the BST becomes unbalanced as the Balance Factor of H is -2. Since the BST is right-skewed, we will perform RR Rotation on node H.
The resultant balance tree is
Insert B, A
On inserting the above elements, especially in case of A, the BST becomes unbalanced as the Balance Factor of H and I is 2, we consider the first node from the last inserted node i.e. H. Since the BST from H is left-skewed, we will perform LL Rotation on node H.
The resultant balance tree is
Insert E
On inserting E, BST becomes unbalanced as the Balance Factor of I is 2, since if we travel from E to I we find that it is inserted in the left subtree of right subtree of I, we will perform LR Rotation on node I. LR = RR + LL rotation
a) We first perform RR rotation on node B
The resultant tree after RR rotation is
b) We first perform LL rotation on the node I
The resultant balanced tree after LL rotation is
Insert C, F, D
On inserting C, F, D, BST becomes unbalanced as the Balance Factor of B and H is -2, since if we travel from D to B we find that it is inserted in the right subtree of left subtree of B, we will perform RL Rotation on node I. RL = LL + RR rotation.
a) We first perform LL rotation on node E
The resultant tree after LL rotation is
b) We then perform RR rotation on node B
The resultant balanced tree after RR rotation is
Insert G
On inserting G, BST become unbalanced as the Balance Factor of H is 2, since if we travel from G to H, we find that it is inserted in the left subtree of right subtree of H, we will perform LR Rotation on node I. LR = RR + LL rotation.
a) We first perform RR rotation on node C
The resultant tree after RR rotation is
b) We then perform LL rotation on node H
The resultant balanced tree after LL rotation is
Insert K
On inserting K, BST becomes unbalanced as the Balance Factor of I is -2. Since the BST is right-skewed from I to K, hence we will perform RR Rotation on the node I.
The resultant balanced tree after RR rotation is
Insert L
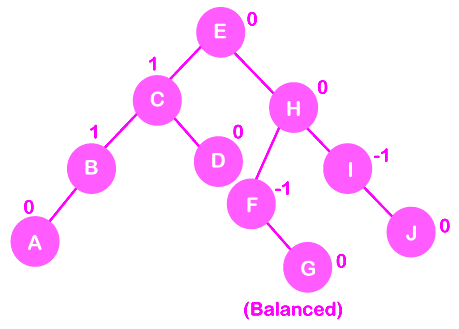
On inserting the L tree is still balanced as the Balance Factor of each node is now either, -1, 0, +1. Hence the tree is a Balanced AVL tree
Construct an AVL tree by inserting the following elements in the given order.
63, 9, 19, 27, 18, 108, 99, 81
The deletion operation in AVL Tree is similar to deletion operation in BST. But after every deletion operation, we need to check with the Balance Factor condition. If the tree is balanced after deletion go for next operation otherwise perform suitable rotation to make the tree Balanced.