B Tree

In search trees like binary search tree, AVL Tree etc., every node contains only one value (key) and a maximum of two children. But there is a special type of search tree called B-Tree in which a node contains more than one value (key) and more than two children. B-Tree was developed in the year 1972 by Bayer with the name Height Balanced m-way Search Tree. Later it was named as B-Tree.

B-Tree can be defined as follows...

B-Tree is a self-balanced search tree in which every node contains multiple keys and has more than two children.

Here, the number of keys in a node and number of children for a node depends on the order of B-Tree. Every B-Tree has an order.

B-Tree of Order m has the following properties...

• Property #1 - All leaf nodes must be at same level.
• Property #2 - All nodes except root must have at least [m/2]-1 keys and maximum of m-1 keys. 

                               m = 4 

                              min keys: 4/2-1 = 1

• Property #3 - All non leaf nodes except root (i.e. all internal nodes) must have at least m/2 children.
• Property #4 - If the root node is a non leaf node, then it must have atleast 2 children.
• Property #5 - A non leaf node with n-1 keys must have n number of children.
• Property #6 - All the key values in a node must be in Ascending Order.

For example, B-Tree of Order 4 contains a maximum of 3 key values in a node and maximum of 4 children for a node.

 m = 4

max keys: 4 – 1 = 3

Example

Operations on a B-Tree

The following operations are performed on a B-Tree...

1. Search
2. Insertion
3. Deletion

 

Search Operation in B-Tree

 

The search operation in B-Tree is similar to the search operation in Binary Search Tree. In a Binary search tree, the search process starts from the root node and we make a 2-way decision every time (we go to either left subtree or right subtree). In B-Tree also search process starts from the root node but here we make an n-way decision every time. Where 'n' is the total number of children the node has. In a B-Tree.

The search operation is performed as follows...

• Step 1 - Read the search element from the user.
• Step 2 - Compare the search element with first key value of root node in the tree.
• Step 3 - If both are matched, then display "Given node is found!!!" and terminate the function
• Step 4 - If both are not matched, then check whether search element is smaller or larger than that key value.
• Step 5 - If search element is smaller, then continue the search process in left subtree.
• Step 6 - If search element is larger, then compare the search element with next key value in the same node and repeate steps 3, 4, 5 and 6 until we find the exact match or until the search element is compared with last key value in the leaf node.
• Step 7 - If the last key value in the leaf node is also not matched then display "Element is not found" and terminate the function.
  

For example, if we search for an item 49 in the following B Tree. The process will something like following :

1. Compare item 49 with root node 78. since 49 < 78 hence, move to its left sub-tree.
2. Since, 40<49<56, traverse right sub-tree of 40.
3. 49>45, move to right. Compare 49.
4. match found, return.

Searching in a B tree depends upon the height of the tree.  

Insertion Operation in B-Tree

In a B-Tree, a new element must be added only at the leaf node. That means, the new keyValue is always attached to the leaf node only. The insertion operation is performed as follows...

• Step 1 - Check whether tree is Empty.
• Step 2 - If tree is Empty, then create a new node with new key value and insert it into the tree as a root node.
• Step 3 - If tree is Not Empty, then find the suitable leaf node to which the new key value is added using Binary Search Tree logic.
• Step 4 - If that leaf node has empty position, add the new key value to that leaf node in ascending order of key value within the node.
• Step 5 - If that leaf node is already full, split that leaf node by sending middle value to its parent node. Repeat the same until the sending value is fixed into a node.
• Step 6 - If the spilting is performed at root node then the middle value becomes new root node for the tree and the height of the tree is increased by one.

Example

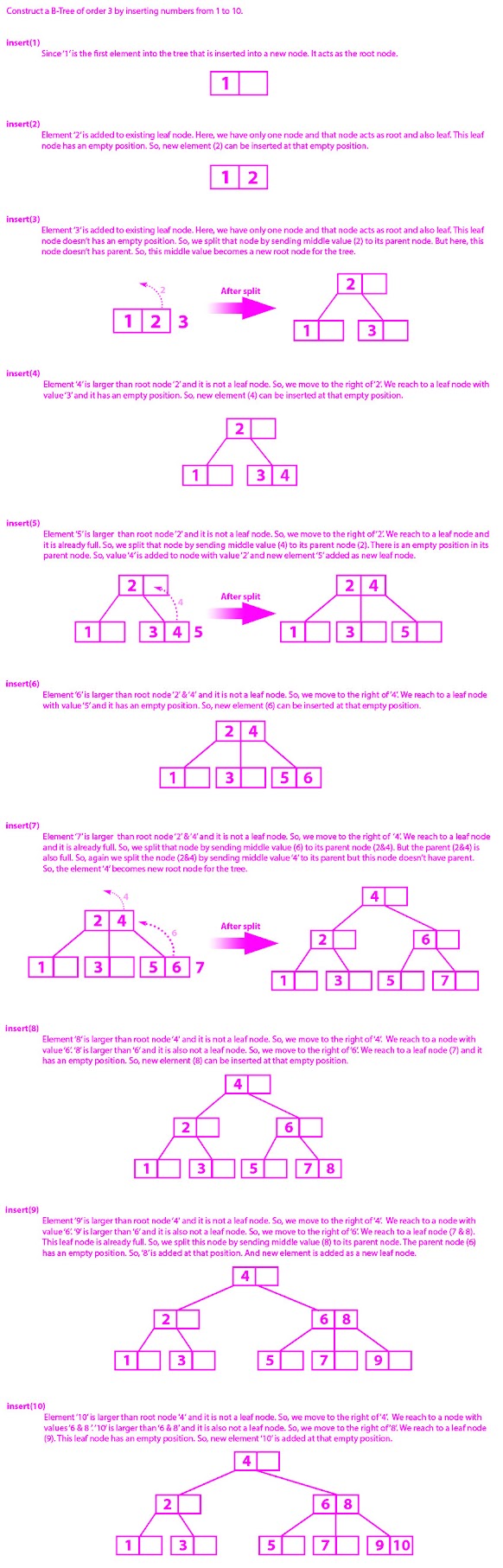
Construct a B-Tree of Order 3 by inserting numbers from 1 to 10.

 

Deletion Operation in B-Tree

Deletion is also performed at the leaf nodes. The node which is to be deleted can either be a leaf node or an internal node. Following algorithm needs to be followed in order to delete a node from a B tree.

1. Locate the leaf node.
2. If there are more than m/2 keys in the leaf node then delete the desired key from the node.
3. If the leaf node doesn't contain m/2 keys then complete the keys by taking the element from eight or left sibling.
• If the left sibling contains more than m/2 elements then push its largest element up to its parent and move the intervening element down to the node where the key is deleted.
• If the right sibling contains more than m/2 elements then push its smallest element up to the parent and move intervening element down to the node where the key is deleted.
4. If neither of the sibling contain more than m/2 elements then create a new leaf node by joining two leaf nodes and the intervening element of the parent node.
5. If parent is left with less than m/2 nodes then, apply the above process on the parent too.

If the the node which is to be deleted is an internal node, then replace the node with its in-order successor or predecessor. Since, successor or predecessor will always be on the leaf node hence, the process will be similar as the node is being deleted from the leaf node.

Example 1

Delete the node 53 from the B Tree of order 5

 

53 is present in the right child of element 49. Delete it. 

 

Now, 57 is the only element which is left in the node, the minimum number of elements that must be present in a B tree of order 5, is 2. it is less than that, the elements in its left and right sub-tree are also not sufficient therefore, merge it with the left sibling and intervening element of parent i.e. 49.

The final B tree is shown as follows. 

 

Application of B tree

B tree is used to index the data and provides fast access to the actual data stored on the disks since, the access to value stored in a large database that is stored on a disk is a very time consuming process.