Binary Search Tree

• Binary Search Tree is a special kind of binary tree in which nodes are arranged in a specific order. This is also called ordered binary tree.
• In a binary search tree, the value of all the nodes in the left sub-tree is less than the value of the root.
• Similarly, value of all the nodes in the right sub-tree is greater than or equal to the value of the root.
• This rule will be recursively applied to all the left and right sub-trees of the root.

 

Number of Binary Search Trees

 

Number of distinct binary search trees possible with n distinct keys =  ²ⁿC_n / n+1

Example

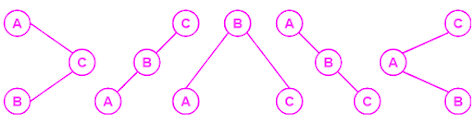
Number of distinct binary search trees possible with 3 distinct keys

= ^2×3C₃ / 3+1

= ⁶C₃ / 4

= 5

 If three distinct keys are A, B and C, then 5 distinct binary search trees are-

 

 

 

Binary Search Tree Construction

 

Example 

 

Construct a Binary Search Tree (BST) for the following sequence of numbers-

50, 70, 60, 20, 90, 10, 40, 100

 

When elements are given in a sequence,

• Always consider the first element as the root node.
• Consider the given elements and insert them in the BST one by one.

 

Insert 50-

Insert 70-

 

As 70 > 50, so insert 70 to the right of 50.

 

Insert 60

  As 60 > 50, so insert 60 to the right of 50.

 As 60 < 70, so insert 60 to the left of 70.

 

 

Insert 20

 

As 20 < 50, so insert 20 to the left of 50.

Insert 90

 

As 90 > 50, so insert 90 to the right of 50.

As 90 > 70, so insert 90 to the right of 70.

 

Insert 10

 

As 10 < 50, so insert 10 to the left of 50.

As 10 < 20, so insert 10 to the left of 20. 

 

Insert 40

 

As 40 < 50, so insert 40 to the left of 50.

As 40 > 20, so insert 40 to the right of 20. 

 

Insert 100

 

As 100 > 50, so insert 100 to the right of 50.

As 100 > 70, so insert 100 to the right of 70.

As 100 > 90, so insert 100 to the right of 90. 

 

 

Example 

 

Construct a Binary Search Tree (BST) for the following sequence of numbers-

43, 10, 79, 90, 12, 54, 11, 9, 50

 

Solution:

 

Example 

 

Construct a Binary Search Tree (BST) for the following sequence of numbers-

10,12,5,4,20,8,7,15 and 13

 

 Solution

 

Problem:

How many distinct binary search trees can be constructed out of 4 distinct keys?

Solution

Number of distinct binary search trees possible with 4 distinct keys

= ²ⁿC_n / n+1

= ^2×4C₄ / 4+1

= ⁸C₄ / 5

= 14