The correct place for easy learning....: Deque

The dequeue stands for Double Ended Queue. In the queue, the insertion takes place from one end while the deletion takes place from another end. The end at which the insertion occurs is known as the rear end whereas the end at which the deletion occurs is known as front end.

Deque is a linear data structure in which the insertion and deletion operations are performed from both ends. We can say that deque is a generalized version of the queue.

Some properties of deque:

Deque can be used both as stack and queue as it allows the insertion and deletion operations on both ends.

In deque, the insertion and deletion operation can be performed from one side. The stack follows the LIFO rule in which both the insertion and deletion can be performed only from one end; therefore, we conclude that deque can be considered as a stack.

In deque, the insertion can be performed on one end, and the deletion can be done on another end. The queue follows the FIFO rule in which the element is inserted on one end and deleted from another end. Therefore, we conclude that the deque can also be considered as the queue.

There are two types of Queues, Input-restricted queue, and output-restricted queue.

Input-restricted queue: The input-restricted queue means that some restrictions are applied to the insertion. In input-restricted queue, the insertion is applied to one end while the deletion is applied from both the ends.

Output-restricted queue: The output-restricted queue means that some restrictions are applied to the deletion operation. In an output-restricted queue, the deletion can be applied only from one end, whereas the insertion is possible from both ends.

Applications of Deque

The deque can be used as a stack and queue; therefore, it can perform both redo and undo operations.
It can be used as a palindrome checker means that if we read the string from both ends, then the string would be the same.
It can be used for multiprocessor scheduling. Suppose we have two processors, and each processor has one process to execute. Each processor is assigned with a process or a job, and each process contains multiple threads. Each processor maintains a deque that contains threads that are ready to execute. The processor executes a process, and if a process creates a child process then that process will be inserted at the front of the deque of the parent process. Suppose the processor P₂ has completed the execution of all its threads then it steals the thread from the rear end of the processor P₁ and adds to the front end of the processor P₂. The processor P₂ will take the thread from the front end; therefore, the deletion takes from both the ends, i.e., front and rear end. This is known as the A-steal algorithm for scheduling.

Implementation of Deque using a circular array

The following are the steps to perform the operations on the Deque:

Enqueue operation

Initially, we are considering that the deque is empty, so both front and rear are set to -1, i.e., f = -1 and r = -1.

As the deque is empty, so inserting an element either from the front or rear end would be the same thing. Suppose we have inserted element 1, then front is equal to 0, and the rear is also equal to 0.

Suppose we want to insert the next element from the rear. To insert the element from the rear end, we first need to increment the rear, i.e., rear=rear+1. Now, the rear is pointing to the second element, and the front is pointing to the first element.

Suppose we are again inserting the element from the rear end. To insert the element, we will first increment the rear, and now rear points to the third element.

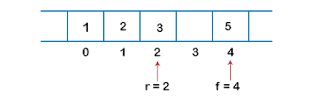
If we want to insert the element from the front end, and insert an element from the front, we have to decrement the value of front by 1. If we decrement the front by 1, then the front points to -1 location, which is not any valid location in an array. So, we set the front as (n -1), which is equal to 4 as n is 5. Once the front is set, we will insert the value as shown in the below figure:

Dequeue Operation

If the front is pointing to the last element of the array, and we want to perform the delete operation from the front. To delete any element from the front, we need to set front=front+1. Currently, the value of the front is equal to 4, and if we increment the value of front, it becomes 5 which is not a valid index. Therefore, we conclude that if front points to the last element, then front is set to 0 in case of delete operation.

If we want to delete the element from rear end then we need to decrement the rear value by 1, i.e., rear=rear-1 as shown in the below figure:

If the rear is pointing to the first element, and we want to delete the element from the rear end then we have to set rear=n-1 where n is the size of the array as shown in the below figure:

Implementation of Double Ended Queue using array

#include <stdio.h>

#define SIZE 5

int deque[SIZE];

int front = -1, rear = -1;

// Insert at front

void insertFront(int value) {

if ((front == 0 && rear == SIZE - 1) || (front == rear + 1))

//The front is just ahead of the rear in a circular fashion front = 3 , rear =2

{

printf("Deque is full (Overflow)\n");

return;

}

if (front == -1) {

front = rear = 0;

} else if (front == 0) {

front = SIZE - 1;

} else {

front--;

}

deque[front] = value;

}

// Insert at rear

void insertRear(int value) {

if ((front == 0 && rear == SIZE - 1) || (front == rear + 1)) {

printf("Deque is full (Overflow)\n");

return;

}

if (front == -1) {

front = rear = 0;

} else if (rear == SIZE - 1) {

rear = 0;

} else {

rear++;

}

deque[rear] = value;

}

// Delete from front

void deleteFront() {

if (front == -1) {

printf("Deque is empty (Underflow)\n");

return;

}

printf("Deleted from front: %d\n", deque[front]);

if (front == rear) {

front = rear = -1;

} else if (front == SIZE - 1) {

front = 0;

} else {

front++;

}

// Delete from rear

void deleteRear() {

if (front == -1) {

printf("Deque is empty (Underflow)\n");

return;

}

printf("Deleted from rear: %d\n", deque[rear]);

if (front == rear) {

front = rear = -1;

} else if (rear == 0) {

rear = SIZE - 1;

} else {

rear--;

}

// Display deque

void display() {

if (front == -1) {

printf("Deque is empty\n");

return;

}

printf("Deque elements: ");

int i = front;

while (1) {

printf("%d ", deque[i]);

if (i == rear)

break;

i = (i + 1) % SIZE;

}

printf("\n");

}

// Main function with user menu

int main() {

int choice, value;

while (1) {

printf("\nDeque Operations Menu:\n");

printf("1. Insert at Front\n");

printf("2. Insert at Rear\n");

printf("3. Delete from Front\n");

printf("4. Delete from Rear\n");

printf("5. Display\n");

printf("6. Exit\n");

printf("Enter your choice: ");

scanf("%d", &choice);

switch (choice) {

case 1:

printf("Enter value to insert at front: ");

scanf("%d", &value);

insertFront(value);

break;

case 2:

printf("Enter value to insert at rear: ");

scanf("%d", &value);

insertRear(value);

break;

case 3:

deleteFront();

break;

case 4:

deleteRear();

break;

case 5:

display();

break;

case 6:

printf("Exiting program.\n");

return 0;

default:

printf("Invalid choice! Please enter a number between 1 and 6.\n");

}

return 0;

}

#include <stdio.h>

#define SIZE 100

int queue[SIZE];

int front = 0, rear = 0;

void enQueueRear();

void enQueueFront();

int deQueueFront();

int deQueueRear();

void display();

int main() {

char ch;

int choice1, choice2, value;

printf("\n******* Type of Double Ended Queue *******\n");

do {

printf("\n1. Input-restricted deque");

printf("\n2. Output-restricted deque");

printf("\nEnter your choice of Queue Type: ");

scanf("%d", &choice1);

switch (choice1) {

case 1: // Input-restricted

do {

printf("\nSelect Operation:");

printf("\n1. Insert (rear)");

printf("\n2. Delete from Rear");

printf("\n3. Delete from Front");

printf("\n4. Display");

printf("\nEnter your choice: ");

scanf("%d", &choice2);

switch (choice2) {

case 1:

enQueueRear();

break;

case 2:

value = deQueueRear();

printf("Deleted from rear: %d\n", value);

break;

case 3:

value = deQueueFront();

printf("Deleted from front: %d\n", value);

break;

case 4:

display();

break;

default:

printf("Invalid choice\n");

}

printf("Do you want to continue this deque? (Y/N): ");

scanf(" %c", &ch);

} while (ch == 'y' || ch == 'Y');

break;

case 2: // Output-restricted

do {

printf("\nSelect Operation:");

printf("\n1. Insert at Rear");

printf("\n2. Insert at Front");

printf("\n3. Delete from Front");

printf("\n4. Display");

printf("\nEnter your choice: ");

scanf("%d", &choice2);

switch (choice2) {

case 1:

enQueueRear();

break;

case 2:

enQueueFront();

break;

case 3:

value = deQueueFront();

printf("Deleted from front: %d\n", value);

break;

case 4:

display();

break;

default:

printf("Invalid choice\n");

}

printf("Do you want to continue this deque? (Y/N): ");

scanf(" %c", &ch);

} while (ch == 'y' || ch == 'Y');

break;

default:

printf("Invalid deque type!\n");

}

printf("\nDo you want to select another deque type? (Y/N): ");

scanf(" %c", &ch);

} while (ch == 'y' || ch == 'Y');

return 0;

}

// Enqueue at Rear

void enQueueRear() {

int value;

if (front == SIZE) {

printf("Queue is full!\n");

return;

}

printf("Enter value to insert at rear: ");

scanf("%d", &value);

queue[front++] = value;

}

// Enqueue at Front

void enQueueFront() {

int value;

if (rear == 0) {

printf("No space at front!\n");

return;

}

printf("Enter value to insert at front: ");

scanf("%d", &value);

queue[--rear] = value;

}

// Dequeue from Front

int deQueueFront() {

if (rear == front) {

printf("Queue is empty!\n");

return -1;

}

return queue[rear++];

}

// Dequeue from Rear

int deQueueRear() {

if (rear == front) {

printf("Queue is empty!\n");

return -1;

}

return queue[--front];

}

// Display Queue

void display() {

if (rear == front) {

printf("Queue is empty!\n");

return;

}

printf("Queue elements: ");

for (int i = rear; i < front; i++) {

printf("%d ", queue[i]);

}

printf("\n");

}

Output

Pages

Deque

Dequeue Operation