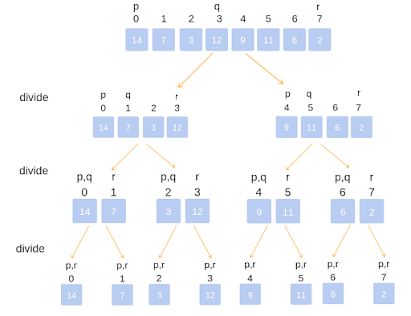
Merge Sort Algorithm

 Merge Sort follows the rule of Divide and Conquer to sort a given set of numbers/elements, recursively, hence consuming less time.

In Merge Sort, the given unsorted array with n elements, is divided into n subarrays, each having one element, because a single element is always sorted in itself. Then, it repeatedly merges these subarrays, to produce new sorted subarrays, and in the end, one complete sorted array is produced.

The concept of Divide and Conquer involves three steps:

1. Divide the problem into multiple small problems.
2. Conquer the subproblems by solving them. The idea is to break down the problem into atomic subproblems, where they are actually solved.
3. Combine the solutions of the subproblems to find the solution of the actual problem.

 

 

Example 

 

 

 

Implementation of Merge Sort Algorithm using C Programming Language

 

     #include<stdio.h>  
    void mergeSort(int[],int,int);  
    void merge(int[],int,int,int);  
    int main ()  
    {   
        int a[30];
        int i,n;
        printf("Enter the number of elements to be sorted: ");
        scanf("%d",&n);  
        for(i=0;i<n;i++)
        {
            printf("Enter element no. %d: ", i+1);
            scanf("%d",&a[i]);
        }
        
        mergeSort(a,0,n-1);  
        printf("printing the sorted elements");  
        for(i=0;i<n;i++)  
        {  
            printf("%d ",a[i]);  
        }  
        return 0;
          
    }  
    void mergeSort(int a[], int beg, int end)  
    {  
        int mid;  
        if(beg<end)  
        {  
            mid = (beg+end)/2;  
            mergeSort(a,beg,mid);  
            mergeSort(a,mid+1,end);  
            merge(a,beg,mid,end);  
        }  
    }  
    void merge(int a[], int beg, int mid, int end)  
    {  
        int i=beg,j=mid+1,k,index = beg;  
        int temp[10];  
        while(i<=mid && j<=end)  
        {  
            if(a[i]<a[j])  
            {  
                temp[index] = a[i];  
                i = i+1;  
            }  
            else   
            {  
                temp[index] = a[j];  
                j = j+1;   
            }  
            index++;  
        }  
        if(i>mid)  
        {  
            while(j<=end)  
            {  
                temp[index] = a[j];  
                index++;  
                j++;  
            }  
        }  
        else   
        {  
            while(i<=mid)  
            {  
                temp[index] = a[i];  
                index++;  
                i++;  
            }  
        }  
        k = beg;  
        while(k<index)  
        {  
            a[k]=temp[k];  
            k++;  
        }  
    } 

Output